Data Structure - Trie - Overview

In computer science, a trie, also called digital tree or prefix tree, is a kind of search tree—an ordered tree data structure used to store a dynamic set or associative array where the keys are usually strings.

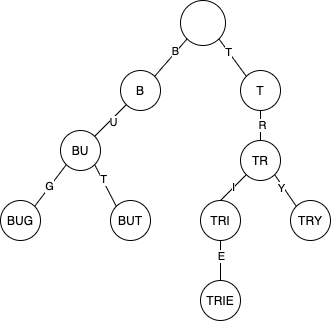
Implement a Basic Trie

Great trie explaination:
https://leetcode.com/problems/implement-trie-prefix-tree/solution/

class TrieNode:
    
    def __init__(self):
        self.next = collections.defaultdict(TrieNode)
        self.is_word = False
        

class Trie:

    def __init__(self):
        self.root = TrieNode()
        

    def insert(self, word: str) -> None:
        """
        Inserts a word into the trie.
        """
        cur = self.root
        for w in word:
            cur = cur.next[w]
        cur.is_word = True
        

    def search(self, word: str) -> bool:
        """
        Returns if the word is in the trie.
        """
        cur = self.root
        for w in word:
            if w not in cur.next:
                return False
            cur = cur.next[w]
        return cur.is_word
        

    def startsWith(self, prefix: str) -> bool:
        """
        Returns if there is any word in the trie that starts with the given prefix.
        """
        cur = self.root
        for w in prefix:
            # print(w, cur.next, cur.is_word)
            if w not in cur.next:
                return False
            cur = cur.next[w]
        return True

Complexity

M is the length of the word

Insert

• time: O(M)
• space: O(M)

Search

• time: O(M)
• space: O(1)

Implement a Trie with Fuzzy Search

A great article here:
https://leetcode.com/problems/design-add-and-search-words-data-structure/solution/

class TrieNode:
    def __init__(self):
        self.next = collections.defaultdict(TrieNode)
        self.isword = False


class WordDictionary:

    def __init__(self):
        self.root = TrieNode()
        

    def addWord(self, word: str) -> None:
        cur = self.root
        for w in word:
            cur = cur.next[w]
        cur.isword = True
        

    def search(self, word: str) -> bool:
        """
        Fuzzy Search
        """
        
        def match(node, word):
            for i, w in enumerate(word):

                if w == '.':
                    # meet . search all children
                    for child in node.next.values():
                        if match(child, word[i+1:]):
                            return True
                    return False

                elif w not in node.next:
                    return False

                else:
                    node = node.next[w]

            return node.isword
        
        return match(self.root, word)

Complexity

M is the length of the word
N is the number of keys in the trie

Insert

• time: O(M)
• space: O(M)

Search

• time: O(N * 26^M)
• space: O(M)

Each word has 26 char, for M length of searched word, need to search 26^M times.
to search all keys, time complexity is O(N * 26^M)

Double-Array Trie

If the trie is static and huge, use Double-Array Trie is very fast to save/load and very fast to lookup. But insert/remove can be costly.
https://linux.thai.net/~thep/datrie/

Reference:

https://en.wikipedia.org/wiki/Trie
https://leetcode.com/problems/implement-trie-prefix-tree/solution/
https://leetcode.com/problems/design-add-and-search-words-data-structure/solution/
https://stackoverflow.com/questions/18963783/build-trie-faster
https://linux.thai.net/~thep/datrie/
https://en.wikipedia.org/wiki/Deterministic_acyclic_finite_state_automaton