A note of Drexel CS520 - CS Foundations
- Deterministic Finite Automaton (DFA)
- Nondeterministic Finite Automaton (NFA)
Deterministic Finite Automaton (DFA)
Deterministic Finite Automaton (DFA) is a theoretical model of Computation
a DFA is a 5-tuple M = (Q,Σ,δ,q,F)
- Q is a finite set of states.
- Σ is a finite set of symbols called the alphabet .
- δ is set of transitions between states.
- q is the start state.
- F a set of accept states. F is a subset of Q.
A DFA is said to accept and input if it exits in an accept state.
The DFA’s memory is limited to its states. It cannot solve problems that require more memory.
Regular Languages
- Languages that DFA can accept are called regular languages
- Infinite Regular Languages must have a repeating component.
- This repetition can be done forever because the DFA has a loop.
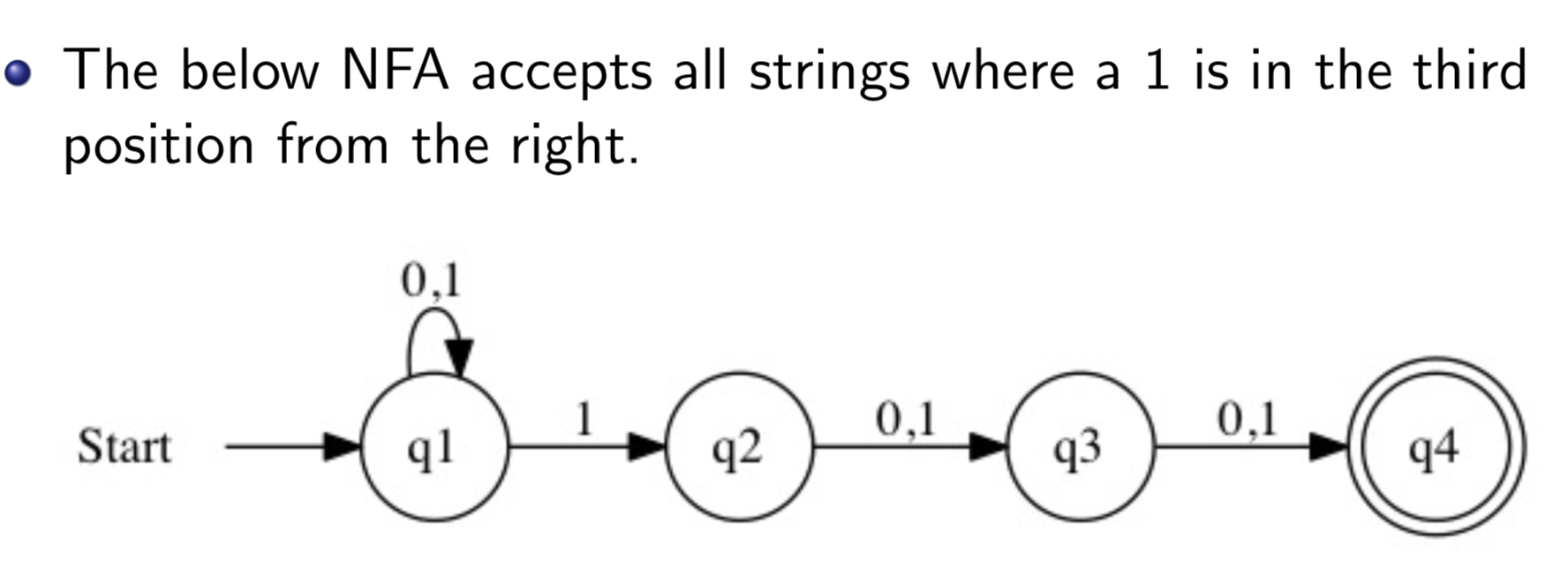
Nondeterministic Finite Automaton (NFA)
Nondeterminism: The ability of a machine to have multiple behaviors given the same input. A NFA can have multiple outgoing edges with the same values. It may have missing edges which are assumed to reject. It may have ε edges that are taken without reading any symbols.
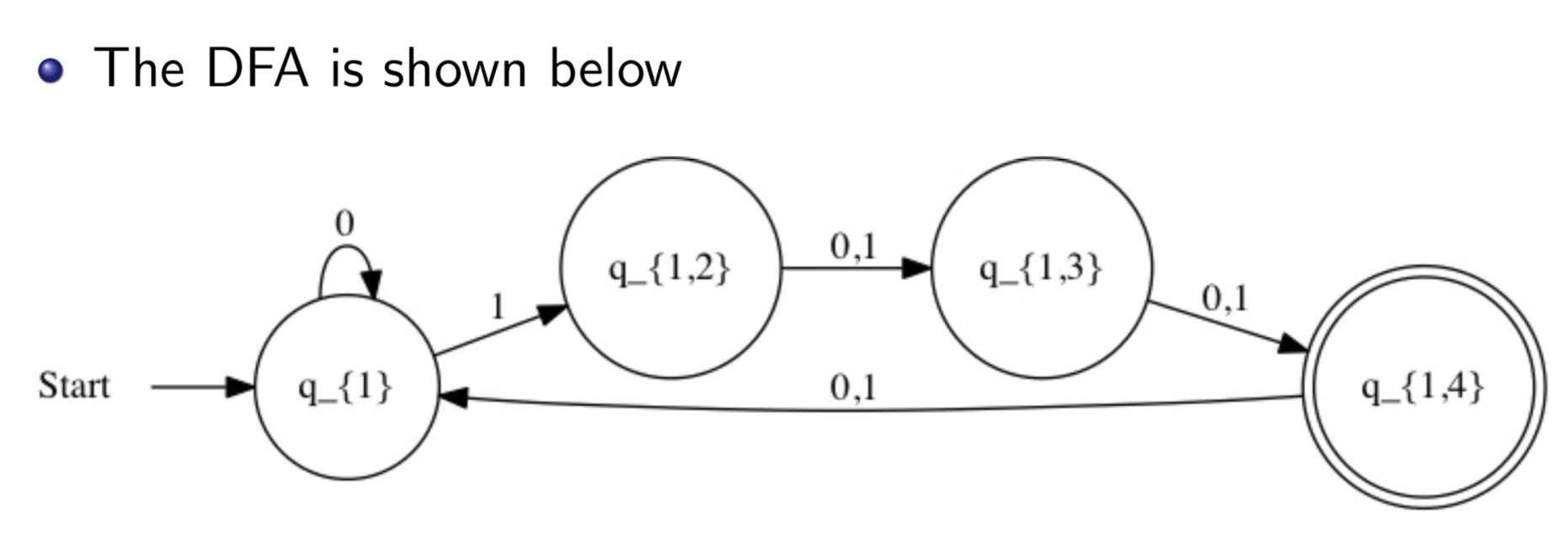
All NFA can be converted to DFA
- Create new states for every combination of original states
- Create a new reject state
- Follow every edge
- If the edges goes into two states, use the new combination states
- If the edges doesn’t exist, point it to the new reject state
- Remove any states that were never used.
- Make accept states
Regular Expressions (RegExp)
Regular Expressions are a simple language to explain text patterns.
Basic Regular Expressions have four components
- Symbols: a single letter to be matched
- Concatenation: Two regexp next to each other need to be found in order
- Union: The | symbol means select either of the two values
- Kleene Star: The ∗ symbol means 0 or more repetitions
A Regular Expression makes a DFA.
Order of Operations: ∗, |, concat
Parenthesis may be used.
All Regular Expressions are DFA
RegExp Examples
- a|b either a or b
- abb only accepts abb
- (a|b)aa accepts aaa or baa
- a*cc accepts cc,acc,aacc,aaacc,aaaaaacc, etc
- (0|1) 101 (1|0) accepts any binary string containing 101
Exercises
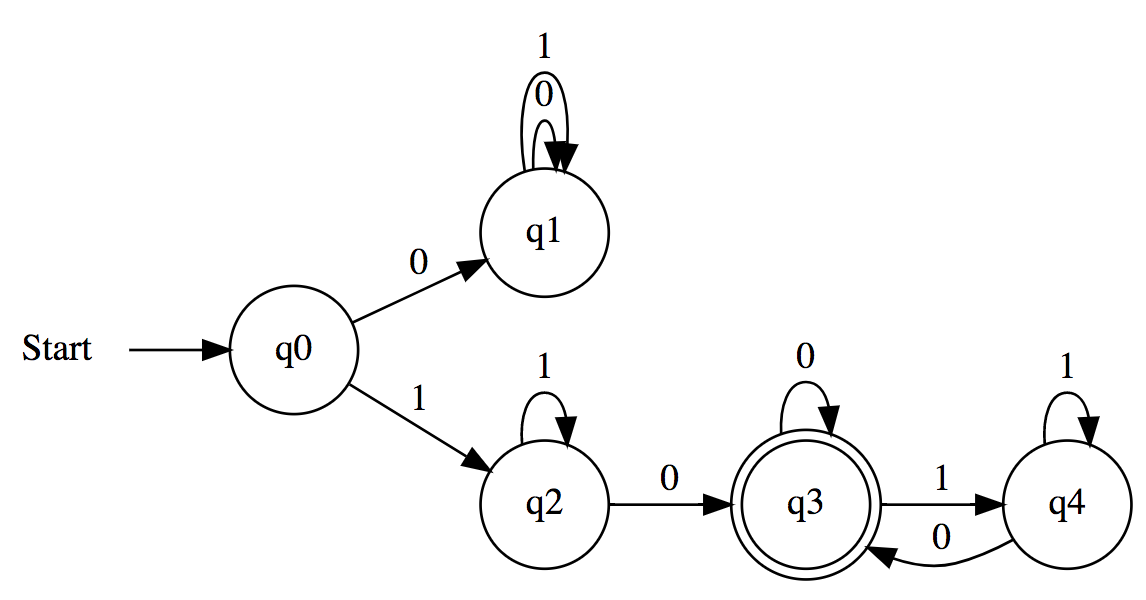
Accepts any binary string containing exactly three 1
1 | # This DFA Accepts the Language |
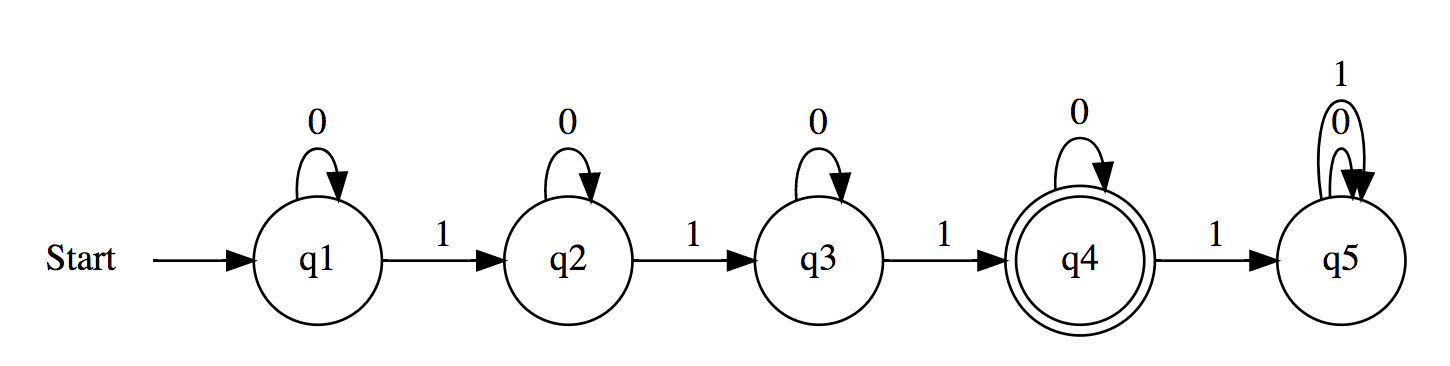
Accepts any binary string whose length is a multiple of 3. (0,3,6,9,…)
1 | # L={ Accepts any binary string containing exactly three 1s } |
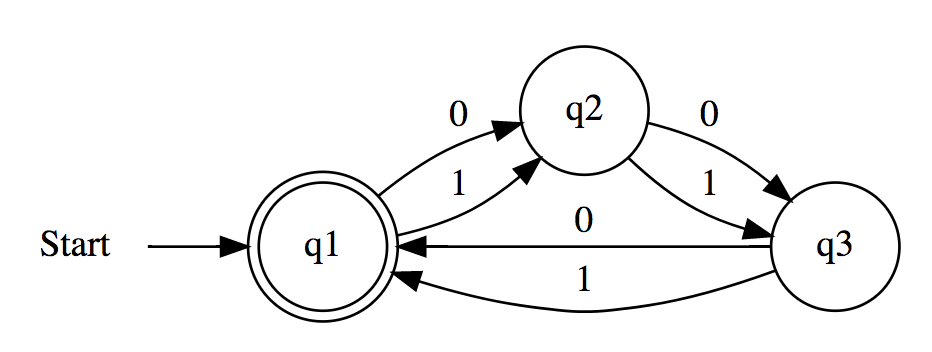
Accepts any binary string that does not contain the substring 110
1 | # L={Accepts any binary string that does not contain the substring 110.} |
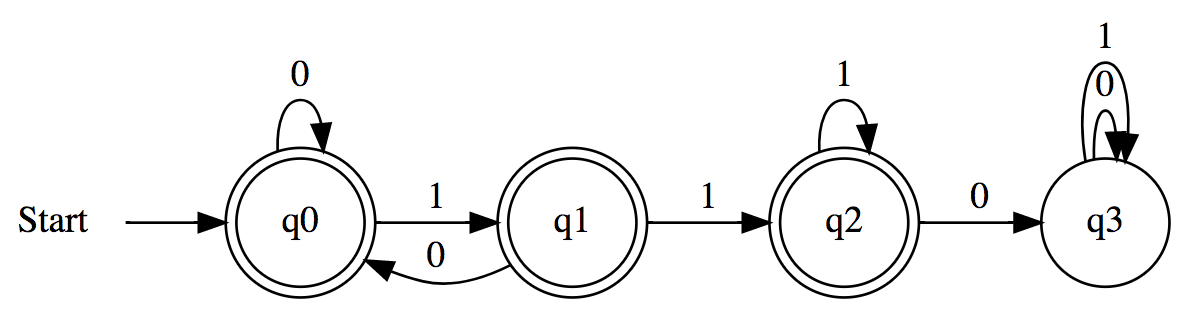
Accepts any binary string that begins with a 1 and ends with a 0
1 | # This DFA Accepts the Language |